IRISAN KERUCUT SEBAGAI KURVA BERDERAJAT DUA
Sebuah kerucut apabila kerucut tersebut dipotong dengan berbagai cara maka akan diperoleh sebuah bidang perpotongan. Hasil irisan pada kerucut tersebut akan membentuk sebuah kurva yang secara umum disebut irisan kerucut (conic section).
Sebuah kerucut apabila kerucut tersebut dipotong dengan berbagai cara maka akan diperoleh sebuah bidang perpotongan. Hasil irisan pada kerucut tersebut akan membentuk sebuah kurva yang secara umum disebut irisan kerucut (conic section).
Kurva berderajat dua atau sering juga disebut irisan kerucut, terdiri dari 4 macam bentuk
1. Lingkaran
2. Elips
3. Parabola
4. Hiperbola
Gambar 1. Irisan Kerucut
Irisan
kerucut memiliki komponen-komponen sebagai berikut;
1. Esentrisitas (e)
Esentrisitas adalah perbandingan jarak titik fokus
ke suatu titik dengan jarak titik tersebut ke garis direktris.
2. Direktris (d)
Direktris adalah sebuah garis yang memiliki jarak
terhadap titik fokus
3. Titik Fokus (F)
Gambar 1. Komponen-komponen pada kurva berderajat dua
Sebuah kurva bidang (plane curve) merupakan himpunan titik-titik yang akan dapat
dinyatakan dalam persamaan kurva. Sebuah persamaan kurva berderajat dua
dinyatakan oleh persamaan berikut :
Ax2
+ By2 + Cxy + Dx + Ey + F = 0
dengan
nilai koefisien A, B, dan C ketiganya tidak bersamaan bernilai nol.
Semua
persamaan berderajat dua seperti di atas, pada sistem koordinat persegi panjang
akan merepresentasikan sebuah kurva yang dinamakan irisan kerucut (conic). Bentuk persamaan kurva
berderajat dua juga dapat dinyatakan sebagai berikut :
ax2
+ by2 + 2hxy + 2gx + 2fy + c = 0
dengan
nilai koefisien a, b, dan h ketiganya tidak bersamaan bernilai nol.
Jika
kurva berderajat dua melalui titik (0, 0) maka diperoleh persamaan kurva yaitu
:
Ax2
+ By2 + Dx + Ey
+ F = 0
dengan
nilai koefisien A dan B keduanya tidak bersamaan bernilai nol
atau
ax2
+ by2 + 2gx + 2fy + c = 0
dengan nilai koefisien a dan b keduanya tidak bersamaan bernilai nol
- PARABOLA
Diberikan suatu titik tertentu f dan garis tertentu D dalam bidang, suatu parabola adalah himpunan semua titik (x, y) sedemikian sehingga jarak antara f dan (x, y) sama dengan jarak antara D dan (x, y). Titik f disebut sebagai fokus parabola dan garis D disebut sebagai direktriks.
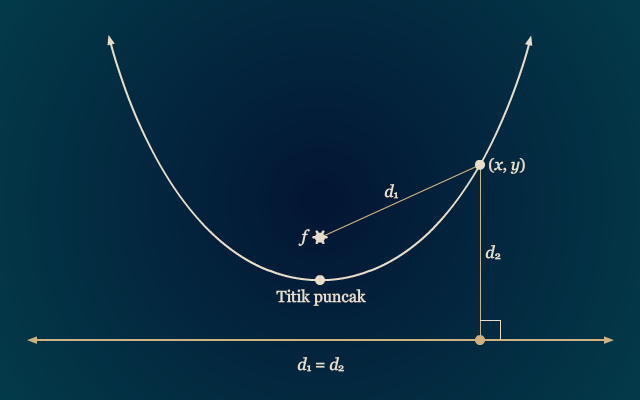
Persamaan umum dari suatu parabola dapat diperoleh dengan mengkombinasikan definisi di atas dan rumus jarak. Dengan tidak mengurangi keumuman, kita dapat menganggap parabola yang ditunjukkan pada gambar di atas memiliki titik puncak di (0, 0) dan memiliki titik fokus di (0, p). Seperti yang ditunjukkan oleh gambar di bawah, parabola yang dimaksud memiliki direktriks dengan persamaan y = –p , sehingga semua titik pada D dapat dituliskan sebagai (x, –p).
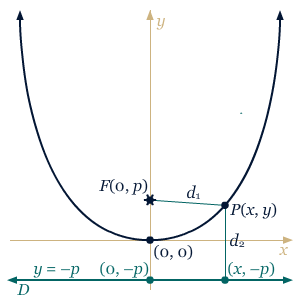
Dengan menggunakan rumus jarak dan menerapkan definisi bahwa d1 = d2, kita mendapatkan,
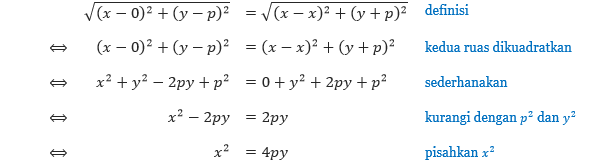
Persamaan terakhir di atas disebut persamaan bentuk fokus-direktriks dari suatu parabola vertikal dengan titik puncak di (0, 0). Jika parabola di atas diputar sehingga terbuka ke kanan, maka kita akan mendapatkan suatu parabola horizontal dengan titik puncak di (0, 0), dan persamaannya adalah y² = 4px.
Persamaan Parabola dalam Bentuk Fokus-Direktriks
Untuk lebih memahami mengenai persamaan suatu parabola dalam bentuk fokus-direktriks, perhatikan contoh berikut.
Suatu parabola vertikal memiliki persamaan dalam bentuk fokus-direktriks: x² = 4py, yang memiliki fokus di (0, p) dan dengan direktriks: y = –p. Jika p > 0, parabola tersebut akan terbuka ke atas. Jika p < 0, parabola tersebut akan terbuka ke bawah.
Suatu parabola horizontal memiliki persamaan dalam bentuk fokus-direktriks: y² = 4px, yang memiliki fokus di (p, 0) dan dengan direktriks: x = –p. Jika p > 0, parabola tersebut akan terbuka ke kanan. Jika p < 0, parabola tersebut akan terbuka ke kiri.
Contoh 1: Menentukan Fokus dan Direktriks dari suatu Parabola
Tentukan titik puncak, fokus, dan direktris dari parabola yang didefinisikan oleh persamaan x² = –12y. Kemudian gambarkan grafiknya, disertai dengan fokus dan direktrisnya.
Pembahasan Karena hanya suku-x yang dikuadratkan dan tidak ada pergeseran yang diterapkan, maka parabola tersebut merupakan parabola vertikal dengan titik puncak di (0, 0). Dengan membandingkan persamaan yang diberikan dengan persamaan umum parabola bentuk fokus-direktriks kita dapat menentukan nilai p:

Karena p = –3 (p < 0), maka parabola tersebut terbuka ke bawah, dengan titik fokus di (0, –3) dan direktriksnya y = 3. Untuk menggambar grafiknya, kita perlu beberapa titik tambahan yang dilalui oleh parabola tersebut. Karena 36 = 6² dapat dibagi oleh 12, maka kita dapat mensubstitusikan x = 6 dan x = –6, dan menghasilkan titik-titik (6, –3) dan (–6, –3). Sehingga grafik dari parabola tersebut dapat digambarkan sebagai berikut.

Dari grafik di atas, kita dapat mengetahui bahwa garis x = 0 merupakan sumbu simetri dari grafik parabola yang diberikan.
Sebagai titik-titik alternatif dalam menggambar grafik parabola, kita dapat menggunakan apa yang disebut tali busur fokus dari parabola. Serupa dengan elips dan hiperbola, tali busur fokus adalah ruas garis yang melalui fokus, sejajar dengan direktriks, dan titik-titik ujungnya terletak pada grafik. Dengan menggunakan definisi dari parabola, jarak horizontal dari f ke (x, y) adalah 2p. Karena d1 = d2, maka ruas garis yang sejajar dengan direktriks dari fokus ke grafik memiliki panjang |2p|, dan panjang tali busur fokus dari sembarang parabola adalah |4p|.
Dan akhirnya, jika titik puncak dari suatu parabola vertikal digeser ke (h, k), maka persamaan dari parabola tersebut akan menjadi (x ± h)2 = 4p(y ± k). Seperti pada keluarga irisan kerucut lainnya, pergeseran vertikal dan horizontalnya berlawanan dengan tandanya (positif atau negatif).
- ELIPS
Elips adalah himpunan titik-titik yang jumlah jaraknya terhadap dua titik tertentu tetap besarnya.a. Ellips with horizontal major axis
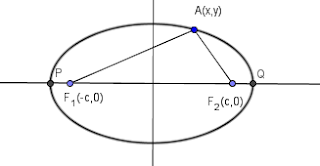
Gambar 1. Elips dengan horizontal major axisKET:F1 dan F2 adalah titik fokus elipsP dan Q adalah titik acuan à |PQ| = 2aDari definisi elips, kita dapat mencari persamaan elips. Misalkan titik-titik fokus F1 ,F2 pada sumbu x dan sumbu dari F1F2 adalah sumbu y. Jika |F1F2| = 2c maka F1(-c,0) dan F2(c,0). Misalkan jumlah jarak yang tetap itu adalah 2a dengan a > c.Dengan A(x,y) sebarang titik yang memenuhi definisi, yaitu:b. Ellips with vertical major axisGambar 2. Elips dengan vertical major axisPersamaan elips dengan vertical major axis adalah,c. Elips horizontal dengan titik pusat (h,k)Gambar 3. Elips horizontal major axis dengan titik pusat (h,k)Persamaan elips dengan vertical major axis adalah,d. Elips horizontal dengan titik pusat (h,k)Gambar 4. Elips vertical major axis dengan titik pusat (h,k)Persamaan elips dengan vertical major axis adalah,GARIS SINGGUNG ELIPS
Gambar 5. Garis Singgung pada Elips
Suatu garis lurus dapat memotong elips, menyinggung atau tidak memotong dan tidak menyinggung elips. Dalam hal yang terakhri garis dan elips tidak mempunyai titik persekutuan. Kita akan mencari persaman garis singgung yag gradiennya m.
Misalkan persamaan garis yang gradiennya m adalah y = mx + p maka persamaan garis singgungnya:
Garis akan menyinggung elips jika titik-titik potongnya berimpit. Hal ini terjadi apabila persamaan kuadrat di atas mempunyai dua kara yang sama atau apabila diskriminannya sama dengan nol.
Jadi, persamaan garis singgung yang gradiennya m adalah,
PERSAMAAN GARIS SINGGUNG DI TITIK PUSAT (α,β)
Misalkan persamaan elipsDengan menggunakan tarnslasi susunan sumbu, kita memperoleh persamaan garis singgung pada elips yang berpusat P(α,β) dengan gradien m adalah - HIPERBOLA
- Hiperbola adalah tempat kedudukan titik-titik yang selisih jaraknya
terhadap dua titik tertentu selalu tetap. Dua titik tertentu itu disebut
fokus hiperbola.
Gambar tersebut merupakan hiperbola yang berpusat di titik O(0,0).
• F1( -c, 0) dan F2(c, 0) adalah titik fokus hiperbola yang jaraknya 2c. Sementara selisih jarak yang tetap itu adalah 2a.
• Sumbu utama adalah sumbu x, sedangkan sumbu sekawan adalah sumbu y.
• Sumbu mayor adalah A1A2, panjangnya 2a. Sumbu minor adalah B1B2, panjangnya 2b.
• Titik A1 dan A2 disebut titik puncak hiperbola yang merupakan titik potong hiperbola dengan sumbu mayor.
• Lactus rectum adalah garis vertikal yang melalui salah satu fokus, tegak lurus sumbu mayor, dan memotong hiperbola di dua titik. Panjang lactus rektum adalah
• Persamaan asimtot hiperbola adalah2b2a
• Eksentrisitas = e = c/a , dengan e > 1.
• Persamaan garis direktriks adalah
• Ketentuan khusus pada hiperbola yaitu c2 = a2 + b2.
- Persamaan Hiperbola a. Persamaan hiperbola yang berpusat di titik (0, 0)
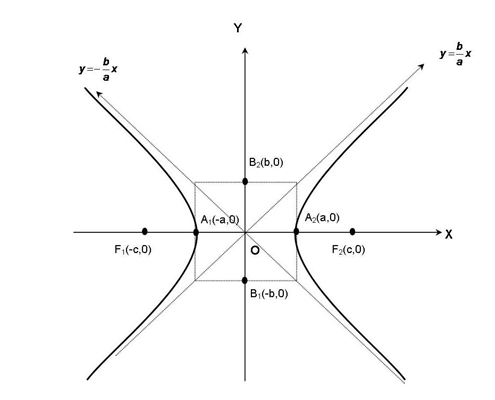
Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu x adalah
Titik fokus adalah F1(c, 0) dan F2(-c, 0).
Titik puncak adalah A1(a, 0) dan A2(-a, 0).
Persamaan asimtotnya adalah
Titik puncak adalah A1(a, 0) dan A2(-a, 0).
Persamaan asimtotnya adalah
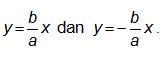
Bagaimana jika sumbu utamanya adalah sumbu y?
Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu y adalah
Persamaan hiperbola yang berpusat di titik (0, 0) dengan sumbu utamanya sumbu y adalah
Titik fokus adalah F1(0, c) dan F2(0, -c).
Titik puncak adalah A1(0, a) dan A2(0, -a).
Persamaan asimtotnya adalah
Titik puncak adalah A1(0, a) dan A2(0, -a).
Persamaan asimtotnya adalah
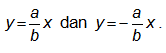
Agar kamu lebih paham, coba cermati contoh soal berikut.
Contoh 1:
Tentukan persaman asimtot dari persamaan
Contoh 1:
Tentukan persaman asimtot dari persamaan
Penyelesaian:
Coba perhatikan bahwa sumbu utama persamaan hiperbola ini adalah sumbu x. Akibatnya, a2 = 9 dan b2 = 16, sehingga a = 3 dan b = 4.
Persamaan asimtotnya adalah
Coba perhatikan bahwa sumbu utama persamaan hiperbola ini adalah sumbu x. Akibatnya, a2 = 9 dan b2 = 16, sehingga a = 3 dan b = 4.
Persamaan asimtotnya adalah

b. Persamaan hiperbola yang berpusat di titik (p, q)

Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utamanya sejajar dengan sumbu x adalah
Titik fokus adalah F1(p + c, q) dan F2(p – c, q).
Titik puncak adalah A1(p + a, q) dan A2(p – a, q).
Persamaan asimtotnya adalah
Titik puncak adalah A1(p + a, q) dan A2(p – a, q).
Persamaan asimtotnya adalah

Bagaimana jika sumbu utama hiperbola sejajar dengan sumbu y?
Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utama sejajar dengan sumbu y adalah
Persamaan hiperbola yang berpusat di titik (p, q) dengan sumbu utama sejajar dengan sumbu y adalah
Titik fokus adalah F1(p, q + c) dan F2(p, q – c)
Titik puncak adalah A1(p, q + a) dan A2(p, q – a).
Titik puncak adalah A1(p, q + a) dan A2(p, q – a).
ersamaan asimtotnya adalah



















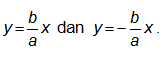
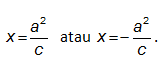
Tidak ada komentar:
Posting Komentar